La sencilla fórmula (maya o no maya) para multiplicar sin calculadora

Existe la extendida creencia de que este método lo inventaron los mayas. El truco matemático que explicamos en este artículo para que realizar multiplicaciones complejas resulte un juego de niños -sin calculadora de por medio- es una sencilla metodología estrictamente gráfica basada en el dibujo de rectas y la contabilización de las intersecciones que crean entre ellas. Matemágicamente, el procedimiento logra obtener el resultado exacto de cualquier multiplicación sin necesidad de saberse ninguna tabla de nuestro sistema decimal.
Existe un debate abierto sobre si el sistema pertenece o no a la cultura prehispánica a la que se le atribuye. Lo cierto es que, aunque existen numerosos sitios en Youtube y otras redes que lo presentan como invención maya, los expertos le dan un origen anónimo a este atajo matemático.
«Una de las razones por la cual me imagino que se comenzó a relacionar este método gráfico con los mayas es por el hecho de que la numeración maya se representaba por medio de puntos, rayas y una concha (cero), y en este método, se trazan líneas y las intersecciones se resaltan con puntos, por lo que algún despistado admirador (que no conocedor) de la cultura maya, lo relacionó», dice Omarklin, colaborador de la plataforma digital Cultura Escéptica.
«Si sabemos del sistema de numeración maya, se puede salir de dudas», añade el rompemitos. «Simplemente hay que darse cuenta de que no se trata del mismo sistema numérico. Por ejemplo, si se tiene una docena de naranjas (funciona igual con manzanas o fresas) se puede escribir como: 12 en un sistema de números arábigo, XII en notación romana, 1100 en un sistema binario, 10 en uno duodecimal, 14 en uno octal, ‘c’ en uno hexadecimal y dos puntos y dos rayas en el Maya, que es vigesimal. Aunque todas las notaciones empleadas representan el mismo número, la misma cantidad de naranjas, cada una de ellas tiene diferente forma de escribir esa cantidad, ya que se han utilizado diferentes sistemas de numeración» prosigue desmitificando el experto.
«Las verdaderas multiplicaciones mayas empleaban un algoritmo diferente al utilizado en nuestro sistema decimal. Aprovechaban una cuadrícula en la que los factores se situaban en la parte externa y se multiplicaban hasta que se iba llenando la cuadrícula al completo. La respuesta de la multiplicación se obtiene a partir de las diagonales de la cuadrícula (como en el método gráfico que erróneamente se atribuye a los mayas), de ahí también puede venir la confusión».
Ya aclarado el background de esta cuenta de la vieja sin origen identificado, maya o no maya, aquí va su explicación. Ya puedes impresionar a tus panzones amigos del cole en la próxima reunión de taberna. Ahora eres el que más rápido multiplica a mano.
Multiplicación para números de dos cifras: 
(Ejemplo: 12 x 13)
Dibuja el 12: Para ello separa sus cifras (1 y 2). Dibuja una línea transversal para representar el 1, y por abajo, separado de ellas, aunque paralelas, otras dos líneas para representar el 2.

 
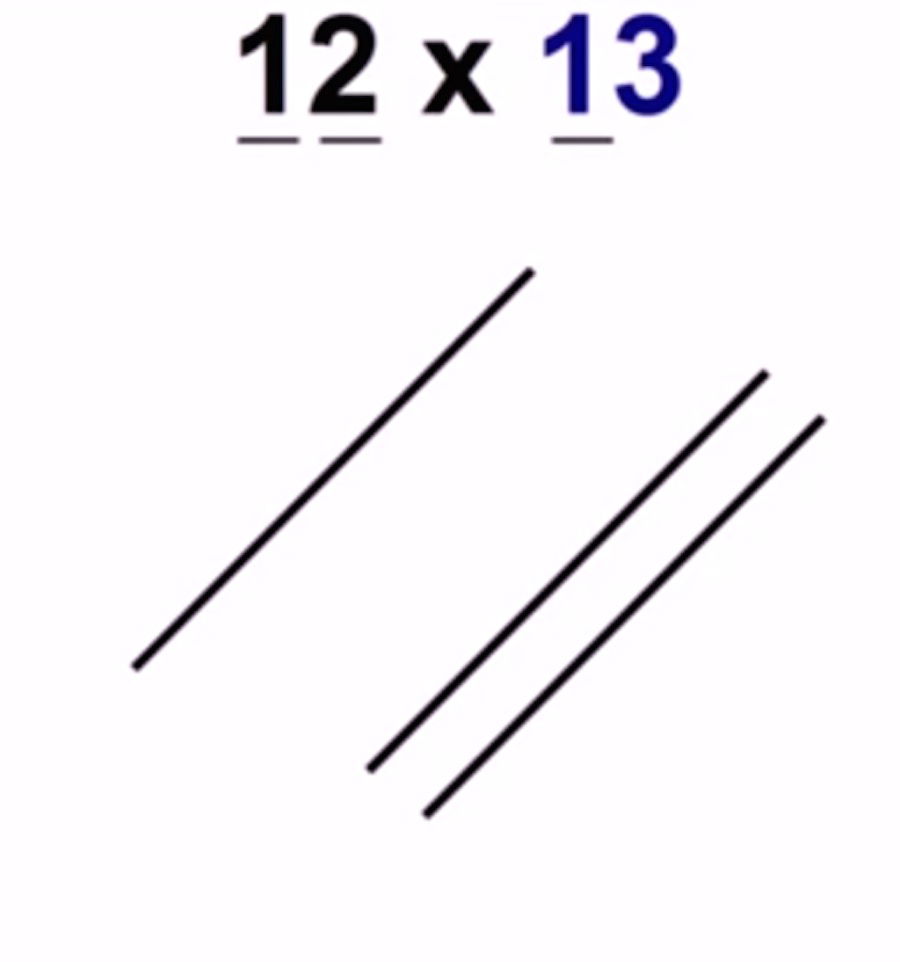
Dibuja el 13: Igualmente separa sus cifras (1 y 3). En sentido perpendicular a las del número has que dibujado primeramente. Esta vez lo harás de abajo a arriba, es decir, dibuja una línea para representar el 1, y arriba, separada de ella, otras tres líneas para representar el 3.
 

 
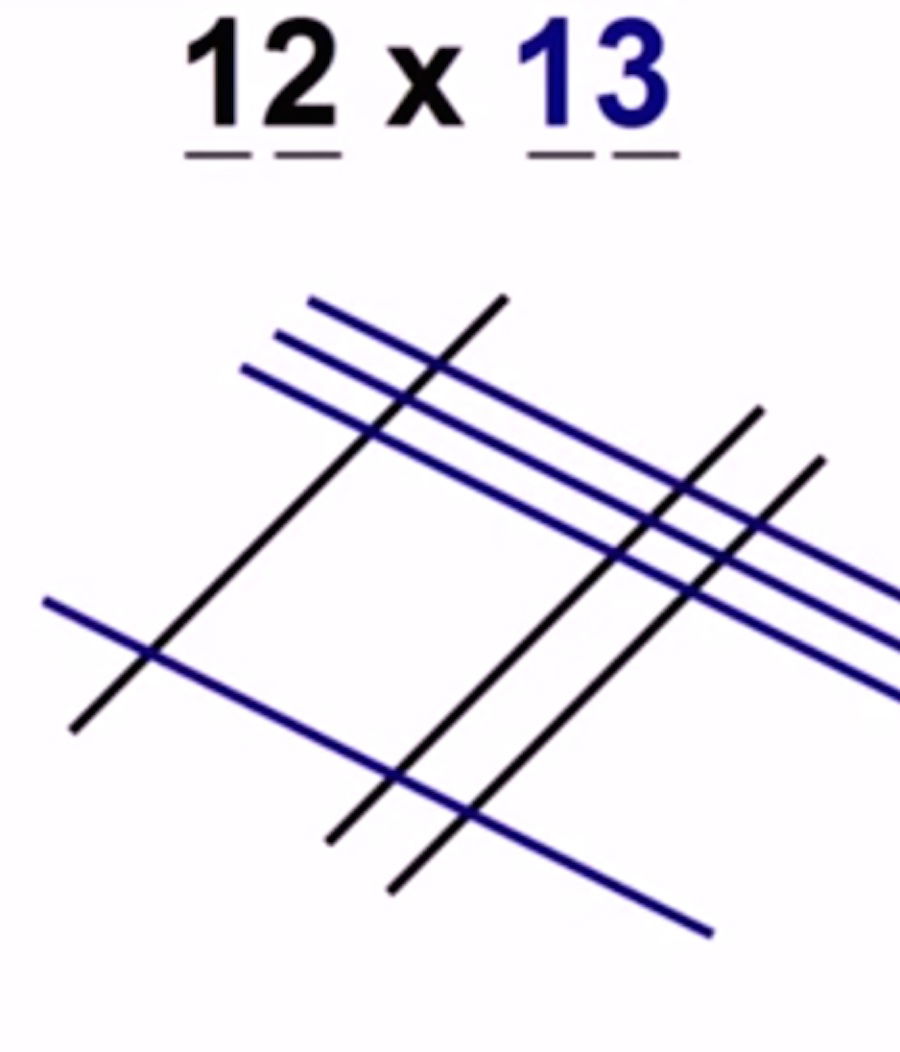
Ahora, teniendo en cuenta la verticalidad de la figura que has formado (que se parece a un cuadrado apoyado en uno de sus picos), separa la imagen en tres columnas imaginarias. Quedará el vértice izquierdo en la columna de la izquierda, dos (el superior y el inferior) en la columna del centro, y el vértice derecho en el de la derecha (Con todos los cortes que implica cada uno de comunes vértices de los que hablamos).

Por último contabiliza el número de cortes (o intersecciones) que se ha formado en cada una de las columnas en las que has dividido la figura.

RESULTADO: 12 x 13 = 156
(¡¡compruebalo con tu calculadora si no te lo crees!!
 
* En caso de que una de las columnas supere la decena al sumar sus puntos:
(Ejemplo 15 x 21)

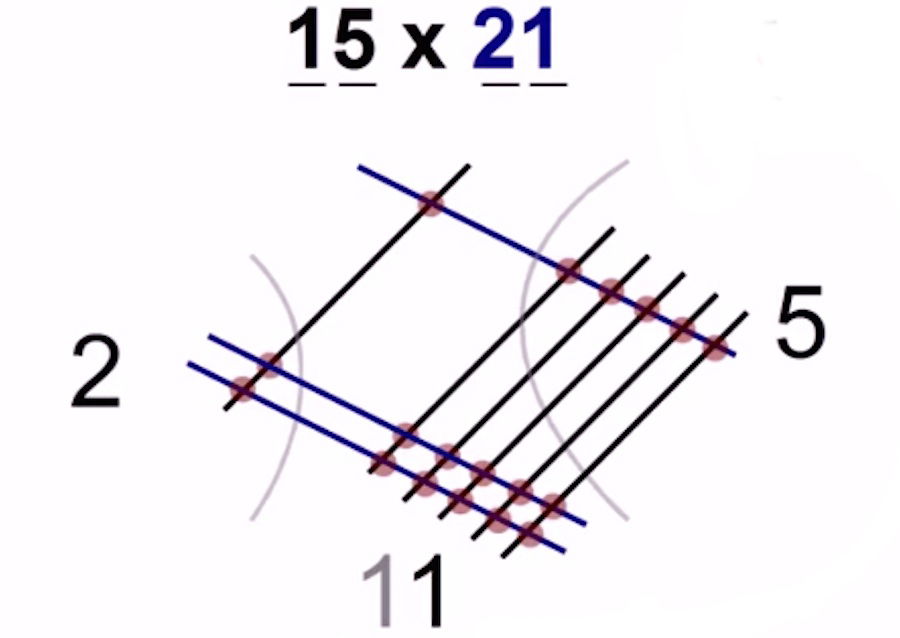
Se pasa una unidad a la columna siguiente

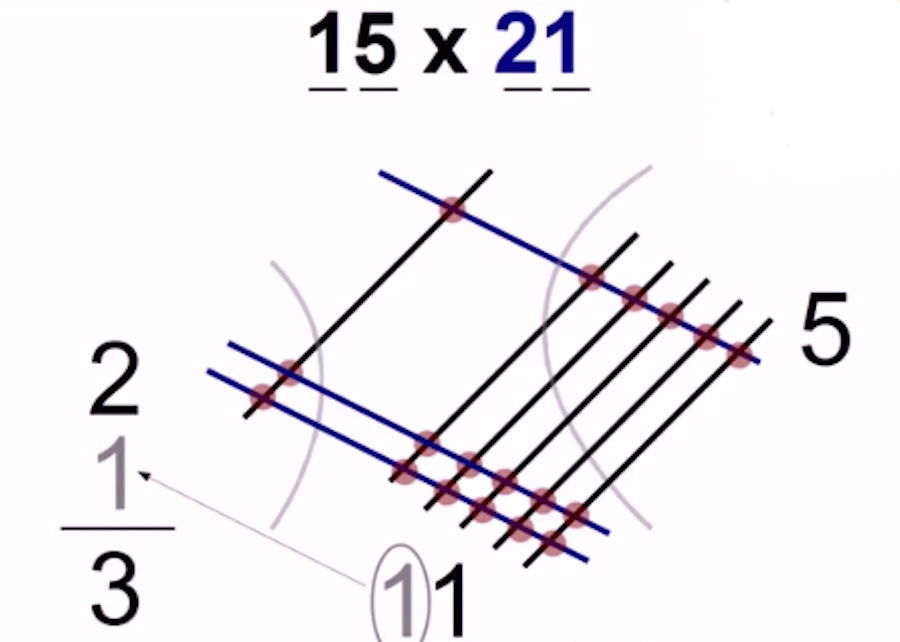
RESULTADO: 15 x 21 = 315
 
Multiplicación para cifras de más números:
(Ejemplo: 123 x 321)
El proceso es el mismo. Simplemente, al haber tres cifras, los grupos de líneas son tres, uno por cifra representada.
(123):

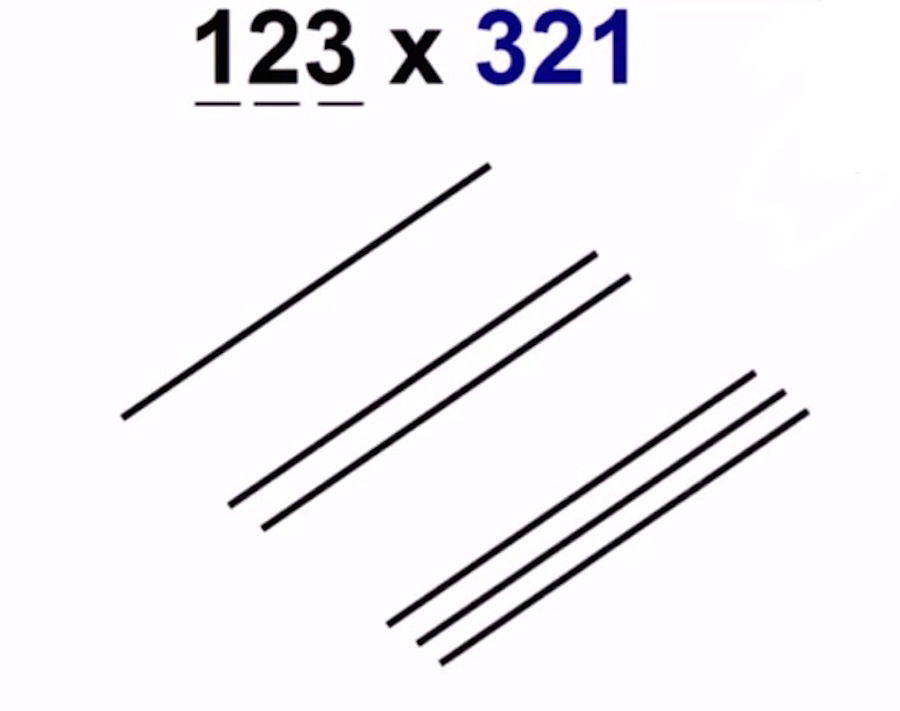
(321):

Al ocurrir esto, las columnas en las que dividimos la imagen, en vez de tres, pasarán a ser 5.
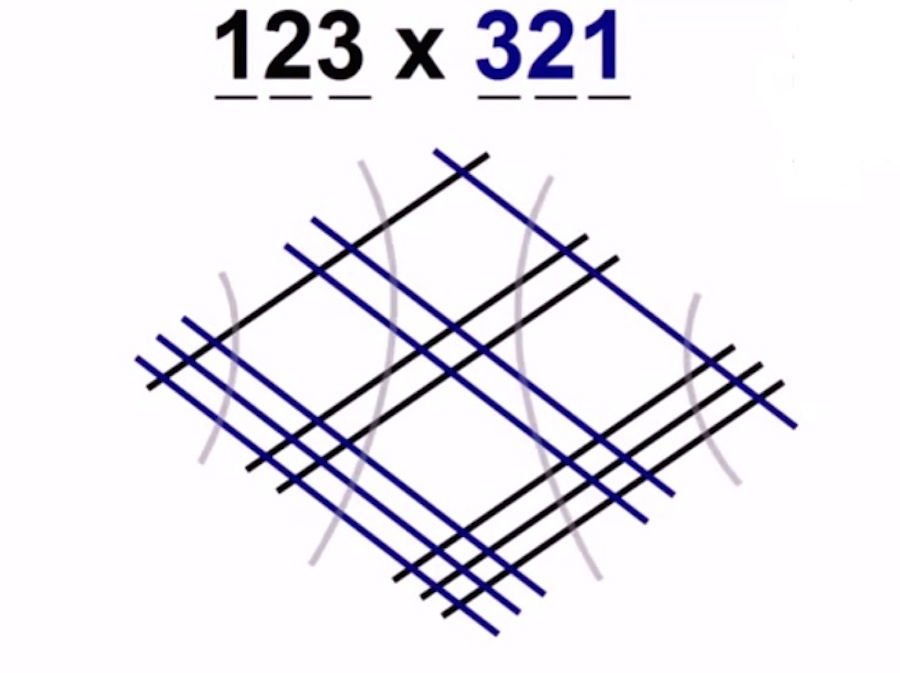Suma los vértices que tienes en cada columna


 
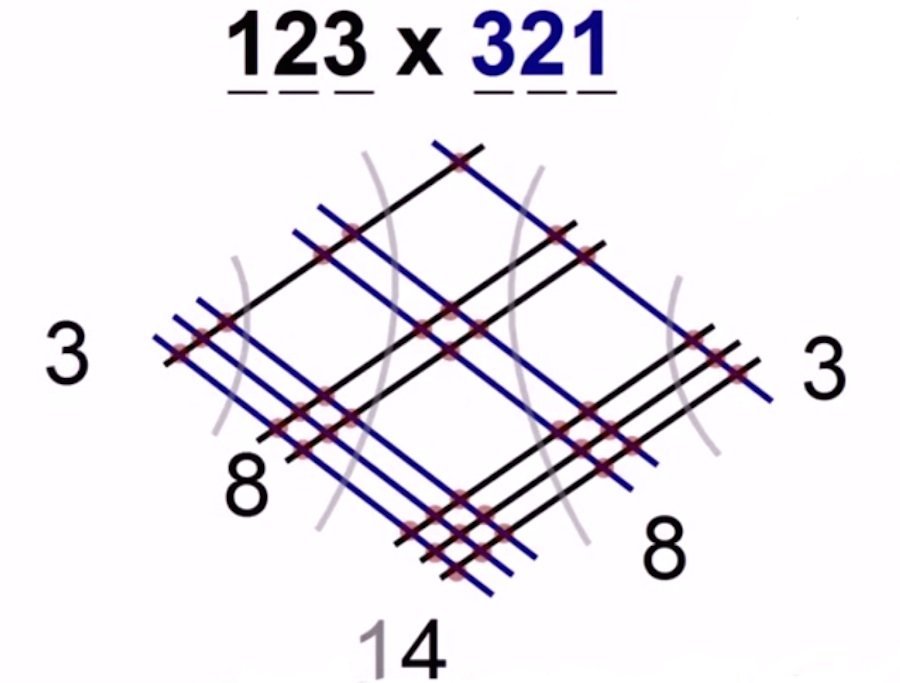
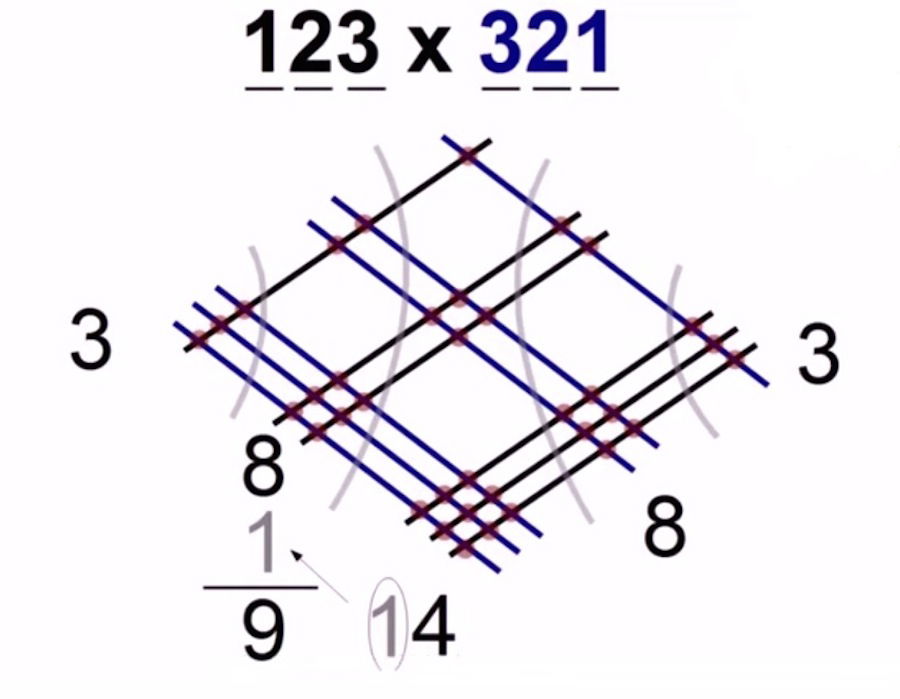
RESULTADO: 123 x 321 = 39483
 
Multiplicación de cifras que incluyan ceros.
(Ejemplo 103 x 221)
Representa el cero con una línea, como si se tratara de un 1, pero dibújalo en diferente color (azul claro).

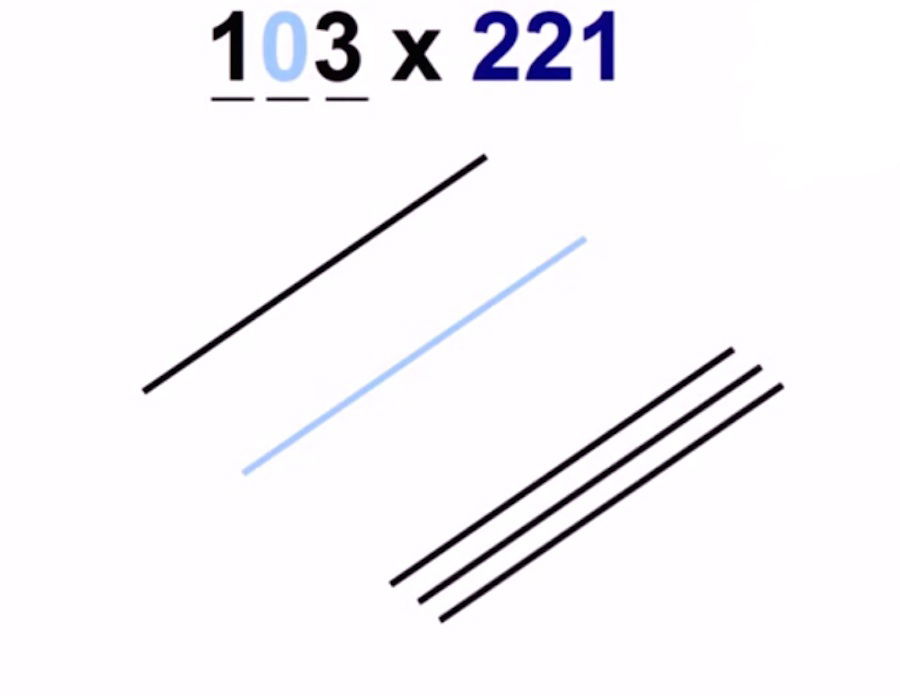
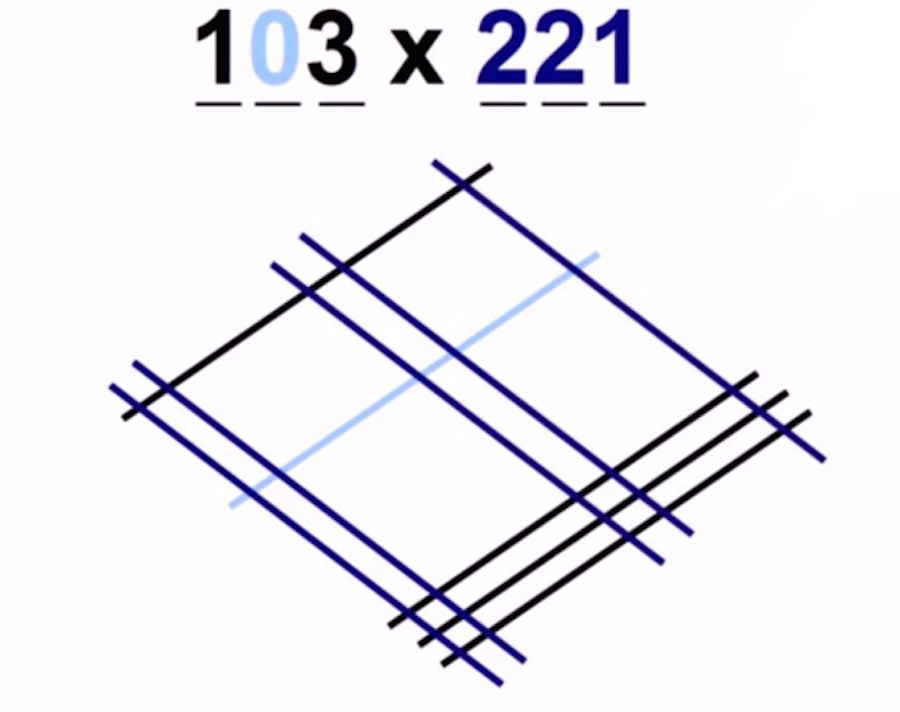
Cuando cuentes los cortes o intersecciones, no tengas en cuenta ninguno en los que una de las líneas sea la línea de otro color (la línea cero)

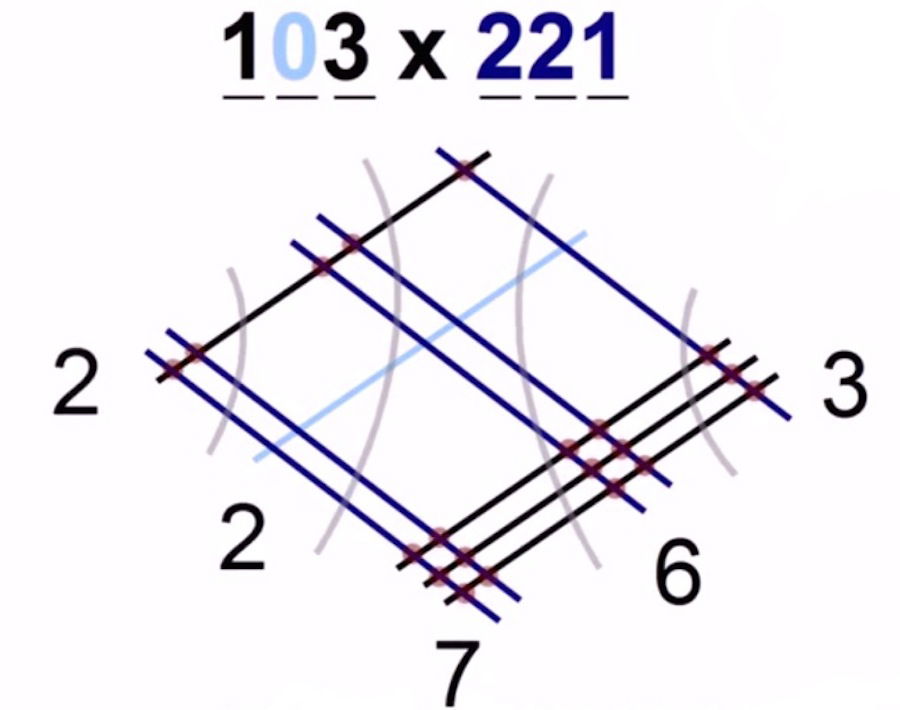
RESULTADO 103 X 221 = 22763
 
El más difícil todavía. ¡Para sumas algebráicas!
Ejemplo: (x + 2y) x (x + 3y)
Toma un color para representar las incógnitas x (negro), y otro para representar las incógnitas y (azul).
El procedimiento es el mismo. Primera cifra de la multiplicación (x + 2y)
1x = 1 línea (negras)
2y = 2 líneas (azules)

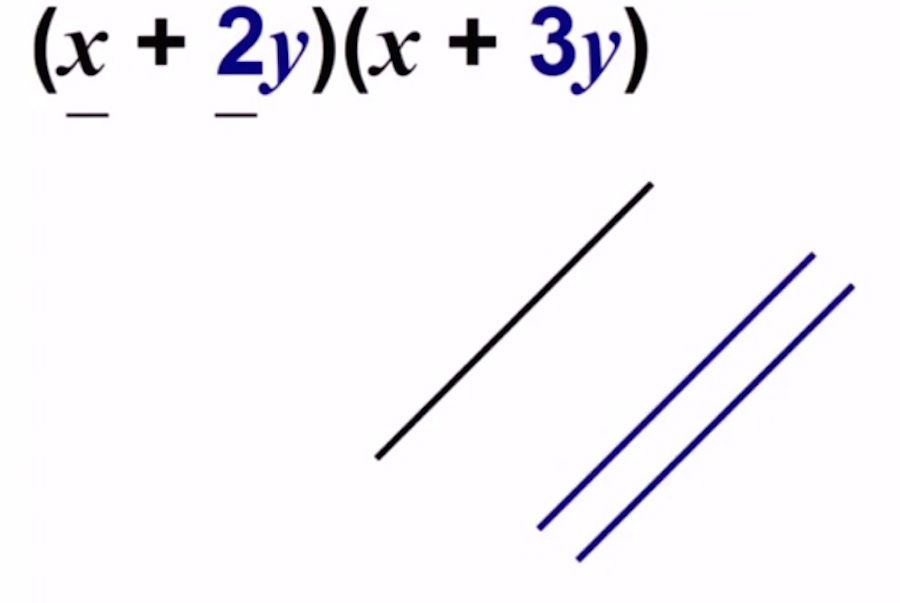
Cruza perpendicularmente las líneas de la segunda cifra de la multiplicación (x + 3y)
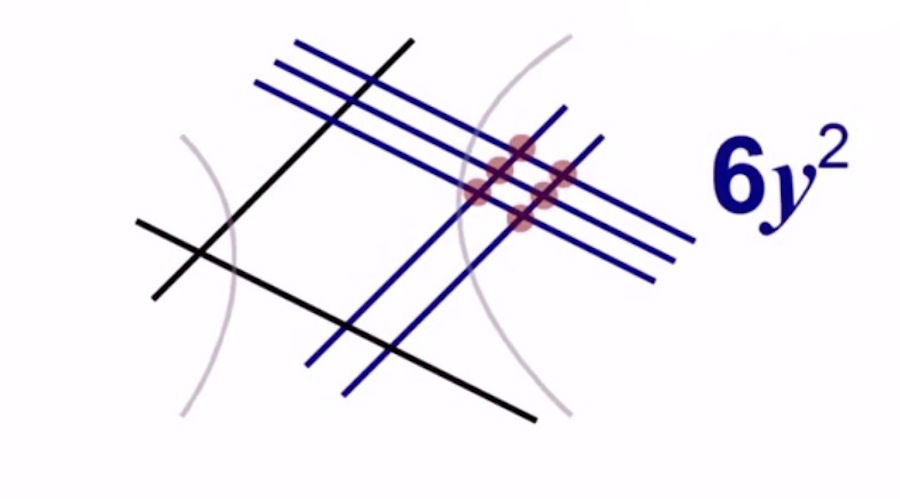
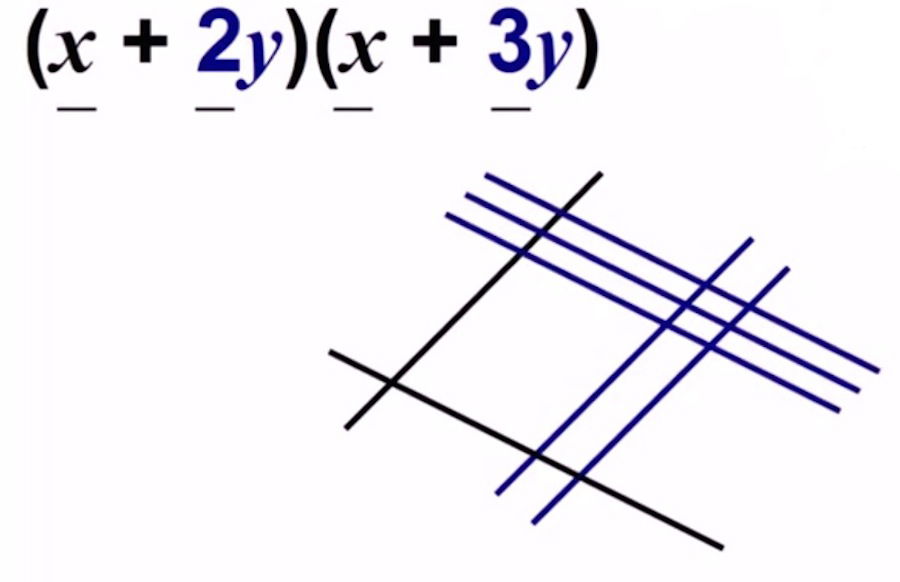A la hora de sumar los puntos o cortes que se han formado en cada columna, fíjate si todas las líneas que interseccionan tienen el mismo color. Si es así, escribe el número de puntos resultantes, la letra que representa ese color, y eleva esa letra al cuadrado.

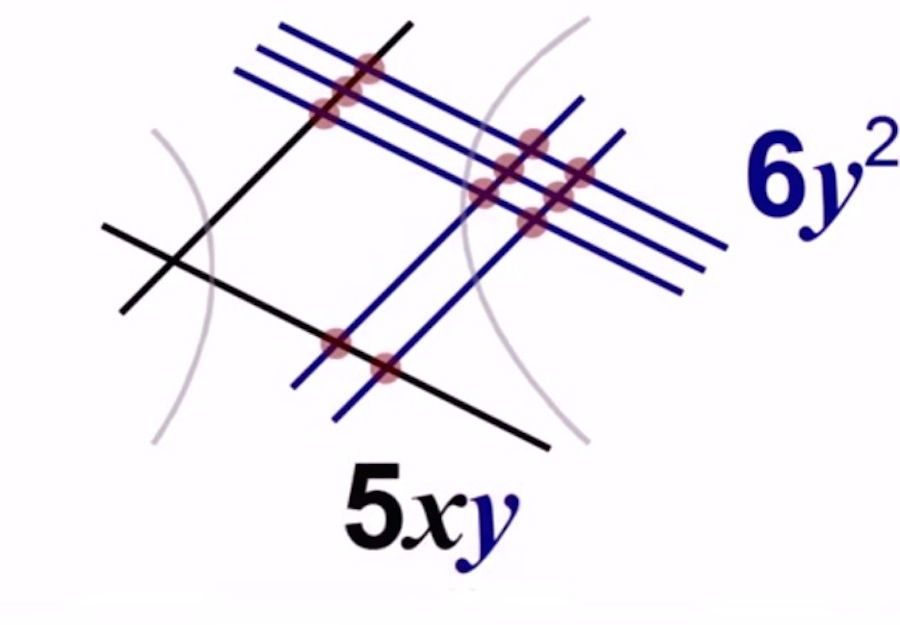
Si en la columna hay cortes creados por líneas de ambos colores, escribe el número de puntos seguido de xy


 
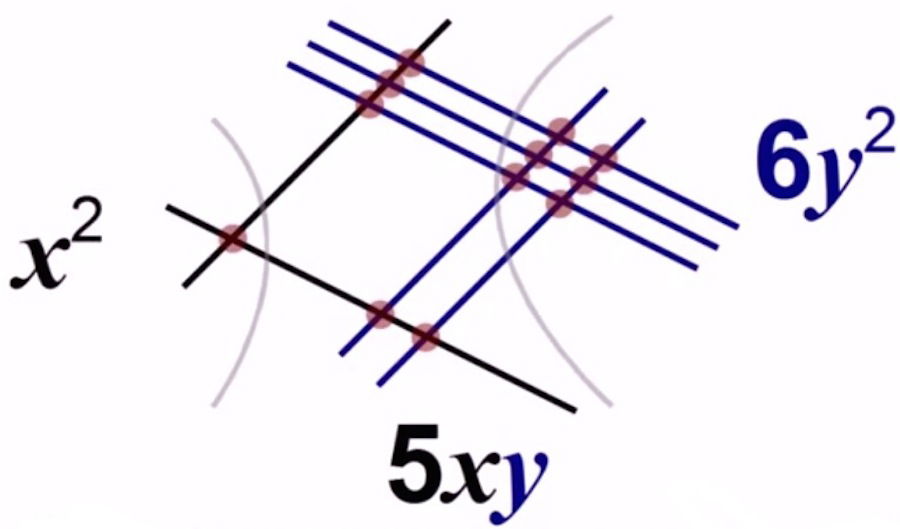
RESULTADO: (x + 2y) x (x + 3y) = x²+5xy + 6y²
*Aquí te dejamos el vídeo desde el que hemos aprendido a hacer esto en Yorokobu.